Egaroucid 技術資料
技術解説
日本語のみでEgaroucidの技術解説を書きました。のんびりと追記します。
ベンチマーク
Egaroucidの性能の確認として2種類のベンチマークを使用しています。1つ目はThe FFO endgame test suiteです。これは、終盤の完全読みにかかる時間に関するベンチマークです。2つ目は対戦です。Egaroucidの過去バージョンの他、他の強豪オセロAIとの対戦として、Edaxとも対戦しました。単純に評価関数の強さを計測するため、bookを使わず、XOTという初期局面集を用いて対戦させました。
The FFO endgame test suite
終盤探索は、以下3つの指標で評価しています。
- 計算時間
- 訪問ノード数
- NPS (1秒あたりのノード訪問回数)
ユーザにとって一番重要なのは計算時間です。決まったテストケースを処理するのにかかる時間を秒数で表します。ここではThe FFO endgame test suiteの40から59番のテストケース(20から34手完全読み)にかかる時間を使いました。これは減ると嬉しい値です。
計算時間を短くするには、まず(厳密に)無駄な探索を減らせば良いです。無駄な探索が多いと訪問ノード数(探索した盤面の数)が増えます。これも減ると嬉しい値です。
計算時間を短くするためのもう一つの観点は、1秒あたりのノード訪問回数を上げることです。これはNodes Per Secondの頭文字を取ってNPSと言われます。これは上がると嬉しい値です。
以下はThe FFO endgame test suiteの40から59番をCore i9 13900Kで実行した結果を、バージョンを横軸に取ってグラフにしたものです。SIMD版を使用しました。
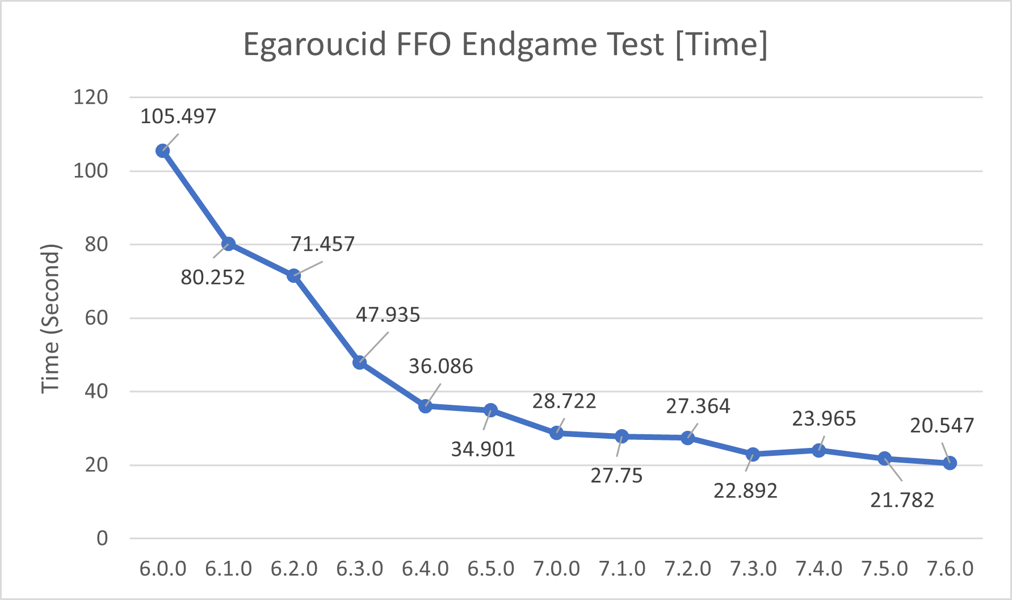
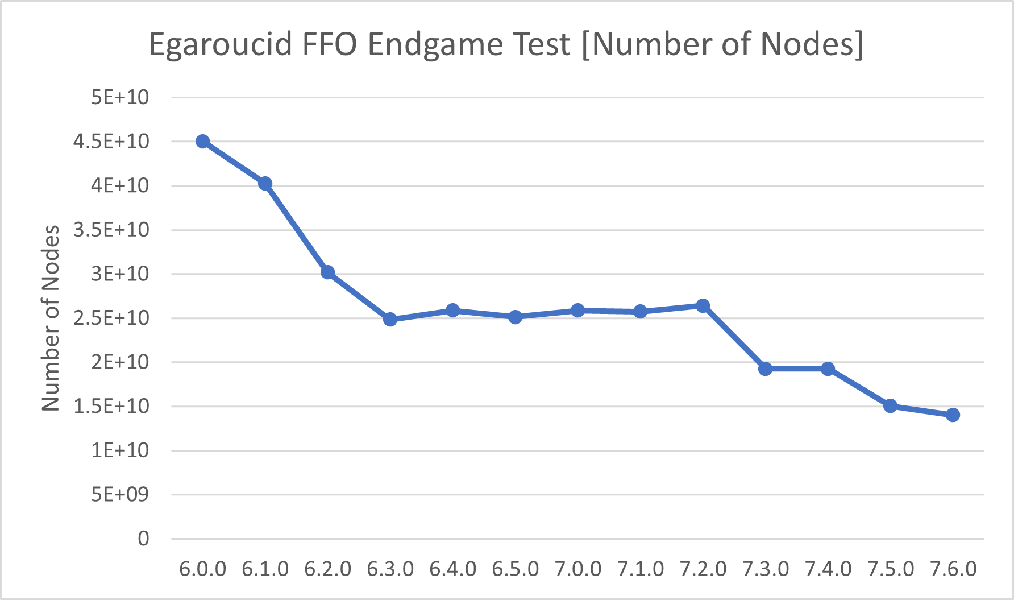
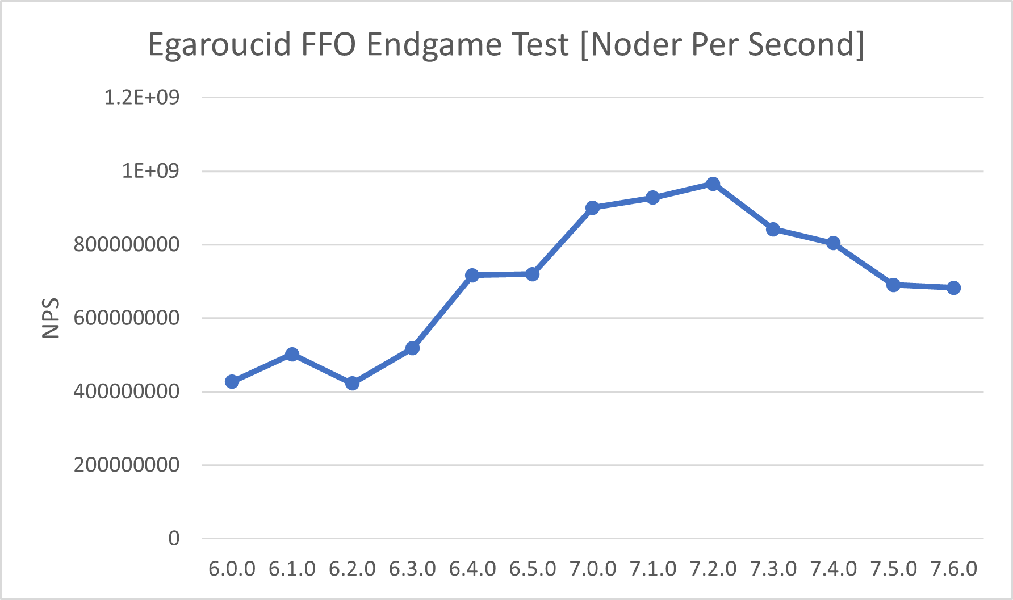
バージョン7.4.0は7.3.0よりも計算時間が多くかかっていますが、これはIntelマイクロコード0x129による性能低下に起因するものです。7.3.0のベンチマーク測定時には0x129適用前でしたが、7.4.0測定時には0x129適用済みでした。
XOTによる対戦
オセロAIの強さを評価するためには、対戦するのが一番でしょう。ここでは、各バージョンにEdax 4.6を加え、総当たり戦をした結果を掲載します。
対戦はレベル1(中盤1手読み、終盤2手完全読み)およびレベル5(中盤5手読み、終盤10手完全読み)で行いました。
対戦にはそれぞれXOTの進行を初期盤面として使い、各進行では先手後手それぞれ1回ずつ対戦させています。
| 名称 | 7.8.0 | 7.7.0 | 7.6.0 | 7.5.0 | 7.4.0 | 7.3.0 | 7.2.0 | 7.1.0 | 7.0.0 | Edax4.6 |
|---|---|---|---|---|---|---|---|---|---|---|
| レベル1 勝率 | 0.5558 | 0.5342 | 0.5676 | 0.5509 | 0.5238 | 0.4844 | 0.4964 | 0.4818 | 0.5058 | 0.2993 |
| レベル1 平均獲得石数 | +2.35 | +1.72 | +2.98 | +2.36 | +0.84 | -0.21 | +0.11 | -0.33 | -0.12 | -9.69 |
| レベル5 勝率 | 0.5836 | 0.5816 | 0.5687 | 0.5711 | 0.5207 | 0.4842 | 0.4924 | 0.5229 | 0.4560 | 0.2189 |
| レベル5 平均獲得石数 | +2.25 | +1.94 | +1.89 | +2.01 | +0.64 | -0.22 | -0.22 | +0.42 | -0.73 | -7.99 |
対戦の詳細はこちらをご覧ください。
バージョンごとの詳細
各バージョンのベンチマークを公開します。上で載せなかった古いバージョンのベンチマークもあります。
こちらの詳細はバージョンごとに少し条件が違うものもありますので、詳細はそれぞれのページをご覧ください。
| バージョン | 7.8.0 | 7.7.0 | 7.6.0 | 7.5.0 | 7.4.0 | 7.3.0 | 7.2.0 | 7.1.0 | 7.0.0 | 6.5.0 | 6.4.0 | 6.3.0 | 6.2.0 | 6.1.0 | 6.0.0 | 5.10.0 | 5.9.0 | 5.8.0 | 5.7.0 | 5.5.0/5.6.0 | 5.4.1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| リリース日 | 2025/12/25 | 2025/08/16 | 2025/04/02 | 2024/12/24 | 2024/10/03 | 2024/08/16 | 2024/06/25 | 2024/06/06 | 2024/04/17 | 2023/10/25 | 2023/09/01 | 2023/07/09 | 2023/03/15 | 2022/12/23 | 2022/10/10 | 2022/06/08 | 2022/06/07 | 2022/05/13 | 2022/03/26 | 2022/03/16 | 2022/03/02 |
学習データ公開
Egaroucidで生成した、オセロAI向け学習データを大量に公開しています。詳しくは学習データをご覧ください。